1. Главная
  2. Библиотека
  3. Высшая математика
  4. В последовательности квадратных трехчленов x^2+ax + b,x^2+(a+1)x+(b+ 1),x^2+(a+2)x +(b+2), . . ., где a – целое число, нек...

В последовательности квадратных трехчленов x^2+ax + b,x^2+(a+1)x+(b+ 1),x^2+(a+2)x +(b+2), . . ., где a – целое число, некоторые два имеют общий корень. Докажите, что все эти трёхчлены имеют корни, и все эти корни - целые числа.

«В последовательности квадратных трехчленов x^2+ax + b,x^2+(a+1)x+(b+ 1),x^2+(a+2)x +(b+2), . . ., где a – целое число, некоторые два имеют общий корень. Докажите, что все эти трёхчлены имеют корни, и все эти корни - целые числа.»
  • Высшая математика

Условие:

1. В последовательности квадратных трехчленов 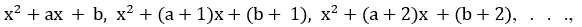где a – целое число, некоторые два имеют общий корень. Докажите, что все эти трёхчлены имеют корни, и все эти корни - целые числа. 

 

2. На стороне треугольника взяты четыре точки К, Р, Н и М, являющиеся соответственно серединой этой стороны, концом биссектрисы противоположного угла треугольника, точкой касания с этой стороной вписанной в треугольник окружности и основанием соответствующей высоты. Найти КН, если КР = а , КМ = b. 

Решение:

1. Пусть трехчлены 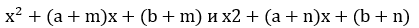имеют общий корень x0. Тогда После тождественных преобразований, получим Но m n 0, поэтому то есть x = 1. Подставляя корень в квадратное уравнение, получаем: откуда b = a1 (целое число). Значит, данные квадратные уравнения имеют вид: Все такие уравнения имеют целые корни:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я