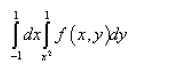
В повторном интеграле ∫_(-1)^1▒dx ∫_(x^2)^1▒f(x,y)dy перейти к полярной системе координат. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y - от параболы x^² до 1.

В повторном интеграле переменная x изменяется от -1 до 1, а переменная y - от параболы x до 1.

Таким образом, область интегрирования снизу ограничена параболой y = x, а сверху - прямой y = 1. Область интегирования изображена на следующем чертеже.

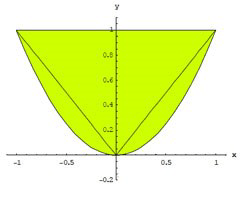
При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторн...