Главная
Библиотека
Высшая математика
В результате эксперимента были получены значения случайной величины Y в зависимости от значений случайной величины X. Резу...

В результате эксперимента были получены значения случайной величины Y в зависимости от значений случайной величины X. Результаты эксперимента представлены в таблице: Построить корреляционное поле и по характеру расположения точек на нем подобрать

«В результате эксперимента были получены значения случайной величины Y в зависимости от значений случайной величины X. Результаты эксперимента представлены в таблице: Построить корреляционное поле и по характеру расположения точек на нем подобрать»

8 ноября 2023
Высшая математика

Условие:

В результате эксперимента были получены значения случайной величины Y в зависимости от значений случайной величины X. Результаты эксперимента представлены в таблице:

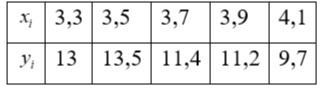
Построить корреляционное поле и по характеру расположения точек на нем подобрать математическую модель регрессионной зависимости Y от X.

Определить параметры уравнения линейной регрессии Y на X.

Проверить значимость коэффициента корреляции при уровне значимости

Определить параметры уравнения линейной регрессии Y на X.

Проверить значимость коэффициента корреляции при уровне значимости α = 0,10.

В случае адекватности построенной модели найти ожидаемые средние значения y при x= 3,8 и при x=4,3.

Решение:

На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.

Линейное уравнение регрессии имеет вид

y = bx + a.

Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид

y = bx + a + ,

где ei наблюдаемые значения (оценки) ошибок i, a и b соответственно оценки параметров и регрессионной модели, которые следует найти.

Для оценки параметров и - используют МНК (метод наименьших квадратов).

Система нормальных уравнений.