В таблицах представлены данные о технико-экономическом показателе X, собранные на одной из дорог ОАО «РЖД» за 2010. В результате первичной обработки данных построен вариационный ряд, проведена группировка, найдены xmin , xmax
- Высшая математика
Условие:
В таблицах представлены данные о технико-экономическом показателе X, собранные на одной из дорог ОАО «РЖД» за 2010. В результате первичной обработки данных построен вариационный ряд, проведена группировка, найдены xmin , xmax (наименьший и наибольший элементы выборки x1, x2, ..., xn из генеральной совокупности X):
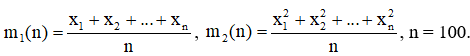
Результаты группировки сведены в таблицу, в которой k – число интервалов разбиения отрезка [xmin , xmax], ni – число точек, попавших в i-й интервал, 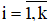 .
.
Исходные данные:

Результаты первичной обработки:
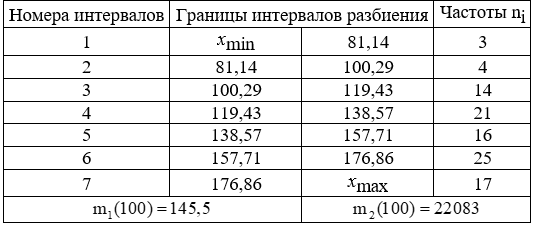
1. Найти размах исходной выборки и числа xmin, x max.
2. Найти выборочные моменты для выборки, составленной из первых 10 элементов исходной выборки, то есть числа m1(10) , m2(10) .
3. По сгруппированной выборке построить гистограмму относительных частот, найти выборочное среднее x̅ и выборочную дисперсию s2.
4. Сравнить гистограмму относительных частот с функцией плотности нормально распределённой случайной величины с параметрами a = x̅, σ = s. Сделать вывод о нормальности генеральной совокупности X, из которой сделана исходная выборка.
Решение:
1. Найдём среди значений признака минимальное и максимальное:
min xi = 62 ,
max xi = 196.
Размах выборки:
R = max xi - min xi = 196 - 62 = 134.
2. Выборочные моменты для выборки, составленной из первых 10 элементов исходной выборки:
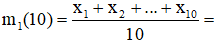
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства