Условие задачи
В таблице №1 приведены длины сторон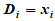 
измеренные светодальномером, и их истинные ошибки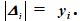 
1) Вычислить оценку коэффициента корреляции между приведенными величинами и определить его значимость и надежность;
2) Получить уравнение регрессии (формулу прогнозов) и оценить точность регрессии;
3) Сделать вывод.
1. Построить поле корреляции (точечную диаграмму), изобразив в прямоугольной системе координат точки с координатами, соответствующими каждой паре наблюдений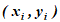 
2. На основании поля корреляции сделать предположение о наличии между случайными величинами X и Y корреляционной зависимости и о форме этой зависимости (линейная или нелинейная).
3. Вычислить оценки математических ожиданий случайных величин X и Y - средние арифметические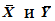 
.
4. Вычислить оценки средних квадратических отклонений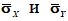 
.
5. Вычислить оценку коэффициента корреляции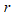 
- выборочный коэффициент корреляции.
6. Проверить гипотезу о не значимости коэффициента корреляции.
7. Оценить надежность коэффициента корреляции (критерий Фишера).
8. Получить уравнение регрессии случайной величины Y на X. Нанести прямую линию регрессии на график.
9. Оценить точность регрессии.
10. Выполнить точечную и интервальную оценку точности параметров уравнения регрессии
11. Сделать общий вывод по результатам анализа.
Ответ
1) Построим поле корреляции:
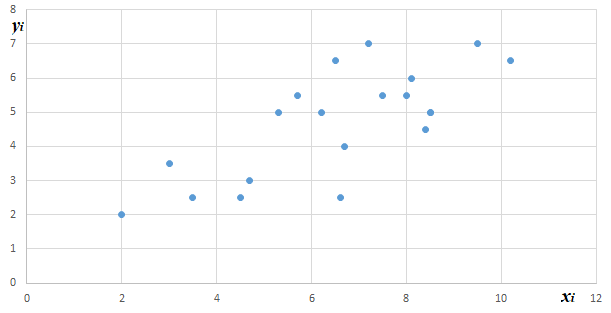
2) Эмпирическая ломаная линия на графике позволяет предположить, что связь выражается прямой линией, т.к. общей тенденцией на графике является направленность эмпирической линии из нижнего левого угла в верхний правый угол. Форма зависимости линейная.
Итак, уравнение регрессии имеет вид:
