Условие:
В таблице приведена выборка значений нормально распределенной случайной величины X. Требуется:
1) найти точечные оценки: для математического ожидания – выборочную среднюю, для дисперсии – выборочную дисперсию (исправленную), для среднего квадратического отклонения – по выборочной дисперсии;
2) записать плотность вероятности и функцию распределения случайной величины X, используя полученные в пункте 1 оценки математического ожидания и дисперсии;
3) с надежностью γ=0,95 найти доверительный интервал для математического ожидания, считая, что дисперсия неизвестна.

Решение:
1). Построим расчетную таблицу:
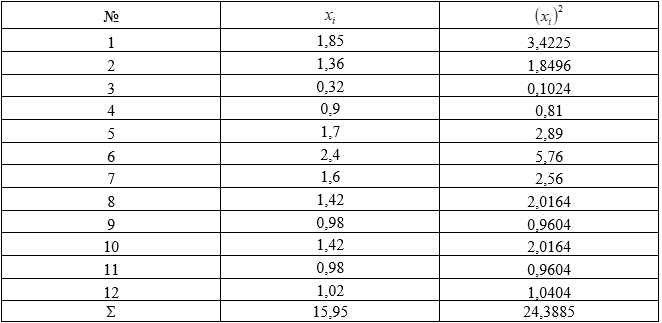
Объем выборки: n = 12.
Выборочная средняя: 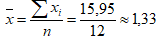 .
.
Выборочная дисперсия: .
