В задаче исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме:
- Высшая математика
Условие:
В задаче исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы возрастания и убывания функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости и точки перегиба графика функции; 6) найти асимптоты графика функции.
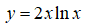
Решение:
1) Найдем область определения функции.
Данная функция определена, если под знаком логарифма стоит число больше нуля, т.е. область определения функции: 
2) Исследовать функцию на непрерывность.
Функция точек разрыва не имеет.
3) Определим, является ли данная функция четной, нечетной.
Данная функция не определена на , поэтому не является ни четной, ни нечетной.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства