1. Главная
  2. Библиотека
  3. Высшая математика
  4. Векторы e1, e2, …, en и икс заданы своими координатами в некотором базисе. Показать, что векторы e1, e2, …, en сами образу...

Векторы e1, e2, …, en и икс заданы своими координатами в некотором базисе. Показать, что векторы e1, e2, …, en сами образуют базис, и найти координаты вектора икс в этом базисе

«Векторы e1, e2, …, en и икс заданы своими координатами в некотором базисе. Показать, что векторы e1, e2, …, en сами образуют базис, и найти координаты вектора икс в этом базисе»
  • Высшая математика

Условие:

Векторы e1, e2, …, en и x заданы своими координатами в некотором базисе. Показать, что векторы e1, e2, …, en  сами образуют базис, и найти координаты вектора x в этом базисе:

а) (1,1,1), 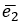=(1,1,2) 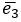= (1,2,3) и 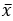= {6,9,14}

б) (2,1,-3), 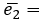(3,2,-5) 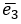=(1,-1,1) и 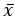={6,2,-7}

 

Решение:

а) Составим определитель из координат векторов e1, e2, e3 и вычислим его по правилу треугольника:

1 * 1* 3+1 * 2 * 1 + 1 * 2 * 1 - ( 1 * 1 * 1 + 1 * 1 * 3 + 2 * 2 * 1)=3 + 2 + 2 -(1 + 3 + 4)=7 - 8 = -1

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я