Условие задачи
Векторы перехода евклидова пространства E4 представлены своими координатами в базисе (a1;a2;a3;a4), векторы которого в свою очередь представлены своими координатами в ортонормированном базисе.
p=(1;1;-1;1), q=(1;2;-1;0), a1=(7;1;-5;-5), a2=(-9;3;17;11), a3=(3;-1;11;13), a4=(1;-7;5;-5)
а) применяя процесс ортогонализации, построить ортонормированный базис b;
б) найти матрицу перехода от базиса a к базису b;
в) найти координаты векторов p, q в ортонормированном базисе b;
г) найти угол между векторами p, q;
Ответ
а)b1'=a1=(7;1;-5;-5);
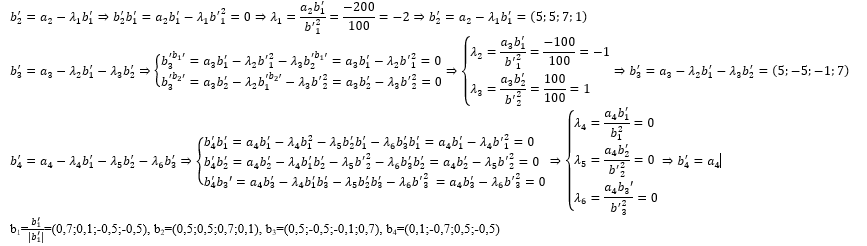
б)









