Решение задачи
Вычислить часть площади поверхности , ограниченной плоскостью .
- Высшая математика
Условие:
Вычислить часть 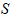 площади поверхности
площади поверхности 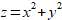 , ограниченной плоскостью
, ограниченной плоскостью 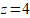 .
.
Решение:
Уравнение задает параболоид вращения с вершиной в начале координат и осью симметрии . В силу осевой симметрии достаточно вычислить площадь поверхности , расположенной в первом октанте, и результат умножить на 4: . Сведем интегрирование по проекции поверхности на координатную плоскость , которая ограничена окружностью, описываемой уравнением, получаемым из уравнения при : -это окружность с центром в начале координат и радиусом . Чтобы свести интегрирование по проекции , необходимо выразить через координаты . Для этого перепишем уравнение поверхности в виде и вычислим направляющий косинус...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э