Условие:
Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а>0).
(x2+y2)2=a2(4x2+y2)
Решение:
Подставляя в исходное уравнениевырадения для x, y вида:
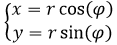
получим:
(r2cos2()+r2sin2())2=a2(4r2cos2()+r2sin...
