Вычислите относительные частоты и накопленные относительные частоты, представьте графически статистический ряд в виде полигона или гистограммы, постройте график накопленных относительных частот.
- Высшая математика
Условие:
1. Постройте статистический ряд.
2. Вычислите относительные частоты и накопленные относительные частоты.
3. Представьте графически статистический ряд в виде полигона или гистограммы.
4. Постройте график накопленных относительных частот.
5. Запишите эмпирическую функцию распределения.
6. Вычислите точечные оценки параметров закона распределения:
- выборочное среднее;
- выборочную дисперсию (смещённую и несмещённую);
- выборочное среднее квадратическое отклонение (смещённое и несмещённое);
- выборочную моду;
-выборочную медиану.
Положим, изучаемая генеральная совокупность подчиняется нормальному закону распределения. Найдите доверительный интервал для неизвестного математического ожидания при условии, что дисперсия неизвестна и доверительная вероятность задаётся формулой  =0.92
=0.92
Для изучения распределения заработной платы работников некоторой отрасли за определенный промежуток времени обследовано 100 человек. Результаты представлены ниже
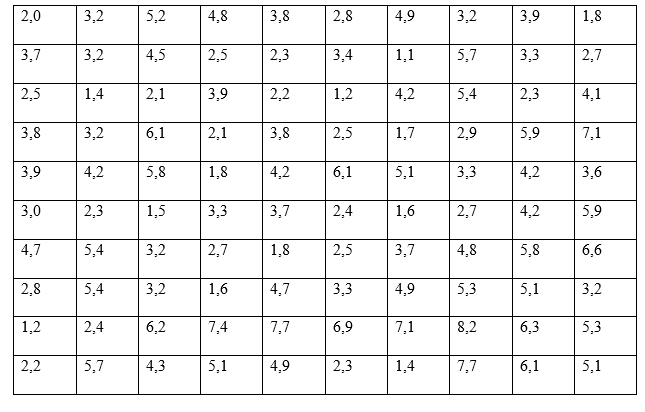
Решение:
1. Построим статистический ряд.
Упорядочим данные по возрастанию и найдем минимальное и максимальное значение в выборке:
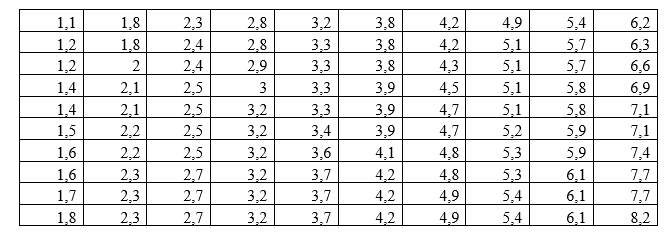
xmin = 1.1, xmax = 8.2
Размах выборки:
r = 8.2 -1.1 = 7.1
Посчитаем количество интервалов, на которые разбивается диапазон, по формуле Стерджеса:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства