Решение задачи
Выразить из системы ограничений базисные неизвестные через параметрические; сформулировать вспомогательную ЗЛП для целевой функции двух аргументов при ограничениях в виде неравенств.
- Высшая математика
Условие:
Решить задачу линейного программирования (ЗЛП)
z=CX → max, где X=[x1 x2 X3 X4 X5]Т
при ограничениях AX=B,
xj ≥ 0 (j=1, ... ,5).
Указание:
1) выразить из системы ограничений базисные неизвестные через параметрические;
2) сформулировать вспомогательную ЗЛП для целевой функции двух аргументов при ограничениях в виде неравенств;
3) решить вспомогательную ЗЛП графическим методом;
4) используя результаты п.1, определить оптимальный план Х для исходной ЗЛП.
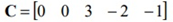
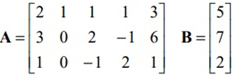
Решение:
Решаем систему АХ = В методом Гаусса относительно неизвестных х1, х2, х3.
Переставим местами 1 и 3 строки. Обозначаем строки расширенной матрицы буквами а1, а2 и а3. В скобках указываем элементарные преобразования.
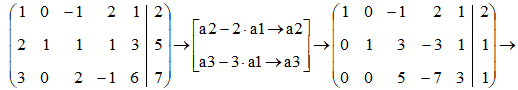
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э