Задача производственного планирования. Решение двумерной задачи графическим способом (графики и расчеты) • Составьте математическую модель исходной задачи.

Задача производственного планирования.

1.     Решение двумерной задачи графическим способом (графики и расчеты)

·        Составьте математическую модель исходной задачи. Опишите экономический (физический) смысл введенных переменных, ограничений задачи и целевой функции.

·        Решите задачу графическим методом по шагам. Выпишите ответ: оптимальный опорный план                      и соответствующее значение целевой функции.

·        Проведите исследование чувствительности найденного плана к изменению параметров задачи (графики и расчеты):

             i.      Определите, какие ограничения задачи являются активными и неактивными в точке    Укажите интервалы устойчивости оптимального плана по отношению к изменению неактивных ограничений.

             ii.      Укажите интервал изменения каждого активного ограничения, в пределах которого его оценка не меняется.

             iii.      Рассчитайте оценки ограничений на ресурсы, характеризующие «вклад» дополнительной единицы ресурса в прирост максимального значения целевой функции.

             iv.      Укажите интервалы устойчивости для каждого коэффициента целевой функции.

2.     Решите задачу в Excel, используя средство «Поиск решения». Проведите анализ Отчетов.

3.     Сравните результаты, полученные в пунктах 1 и 2.

Издательский дом «ОНИКС» выпускает два журнала: «Сделай сам» и «Дом в деревне», которые печатаются в трех типографиях: Типография № 1, Полиграф и АПН, где общее количество часов, отведенной для печати, и производительность печати одной тысячи экземпляров ограничен и представлены в табл.

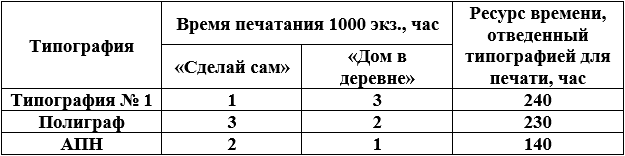
Прибыль от оптовой продажи журналов  «Сделай сам» и «Дом в деревне» соответственно равна 20 и 25 руб./шт. Определите оптимальное количество издаваемых журналов, которое обеспечит максимальную выручку от продажи.