Задана формула логики предикатов A=(x)(P(x)R(x)(y)Q(x,y)) и двухэлементное множество M = {1,2}. Привести формулу A к префиксной нормальной форме. Является ли формула A на множестве M: 1) выполнимой; 2) опровержимой;
- Высшая математика
Условие:
Задана формула логики предикатов
A=(x)(P(x)R(x)(y)Q(x,y))
и двухэлементное множество M = {1,2}. Привести формулу A к префиксной нормальной форме. Является ли формула A на множестве M:
1) выполнимой;
2) опровержимой;
3) общезначимой;
4) невыполнимой?
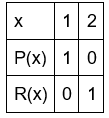
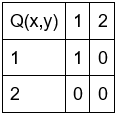
Вычислить значение истинности формулы A на множестве M со следующими предикатами, определенными на M.
Решение:
Интерпретация I = (M={1,2),P,Q,R)
1. Префиксная нормальная форма
A=(x)(P(x)R(x)(y)Q(x,y)) = (x)(P(x)R(x)(y)Q(x,y)) =(x)(y)(P(x)R(x)Q(x,y))
На интерпретации I = (M={1,2),P,Q,R) формула
A=(x)(y)(P(x)R(x)Q(x,y))
2. Элиминация кванторов на конечном множестве M = {1,2}
A=(y)((P(1)R(1)Q(1,y)) (P(2)R(2)Q(2,y))) =(P(1)R(1)Q(1,1)) (P(2)R(2)Q(2,1))
(P(1)R(1)Q(1,2)) (P(2)R(2)Q(2,2))
3. Вычисление значения формулы A на интерпретации I
A(I) = (101)(010)(100)(010) =0111 = 1
4. Пусть x1=P(1), x2=P(2), x3=R(1), x4=R(2), x5=Q(1,1), x6=Q(1,2), x7=Q(2,1), x8=Q(2,2). Тогда
A=(x1x3x5)(x2x4x7) (x1x3x6)(x2x4x8)
При x1 и x2 р...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства