Записать двойной интеграл в виде повторного и изменить порядок интегрирования, если область интегрирования
«Записать двойной интеграл в виде повторного и изменить порядок интегрирования, если область интегрирования»
- Высшая математика
Условие:
Записать двойной интеграл в виде повторного и изменить порядок интегрирования, если область интегрирования
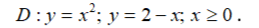
Решение:
Область интегрирования D является правильной (простой) в направлении оси ОУ, т.к. любая прямая, параллельная оси ОУ, пересекает границу области D не более чем двух точках.
Первую точку пересечения с линией у=х2 назовем точкой входа, а линию - линией входа, ее уравнение у=х2. Вторую точку пересечения с линией у=2-х назовем точкой выхода, а линию линией выхода.
Тогда повторный интеграл в правой части составлен из двух определенных:
Первый берется по переменному у, оси которого ОУ параллельны секущие прямые, он называется внутренним. Пределы интегрирования в нем зависят от х и совпадают с ординат...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э