Система состоит из 10 равнонадежных элементов, среднее время безотказной работы элемента mt равно 1000 час. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы
- Автоматика и управление
Условие:
Система состоит из 10 равнонадежных элементов, среднее время безотказной работы элемента mt = 1000 час. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы и основная и резервная системы равнонадежны. Необходимо найти вероятность безотказной работы системы Рс(t), среднее время безотказной работы системы mtс, а также частоту отказов fc(t) и интенсивность отказов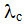 
(t) в момент времени t = 50 час в следующих случаях:
а) нерезервированной системы,
б) дублированной системы при включении резерва по способу замещения (ненагруженный резерв).
Решение:
а) Рассматриваем нерезервированную систему. В этом случае интенсивность отказов не зависит от времени и равна сумме интенсивностей отказов элементов:
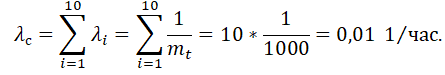
Тогда среднее время безотказной работы такой системы:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства