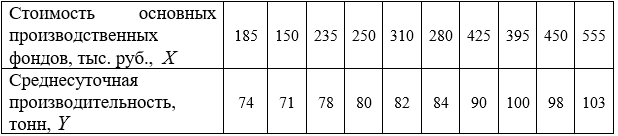
Построить и проинтерпретировать модель взаимосвязи между указанными факторами, проверить на значимость, осуществить точечный и интервальный прогноз, сделать выводы.
- Эконометрика
Условие:
Построить и проинтерпретировать модель взаимосвязи между указанными факторами, проверить на значимость, осуществить точечный и интервальный прогноз, сделать выводы.
1. Исходные данные нанести на координатную плоскость. Сделать предварительное заключение о наличии взаимосвязи между факторами X и Y, о ее характере (положительная или отрицательная) и форме (линейная или нелинейная).
2. Рассчитать значение парного коэффициента корреляции xy r . Используя t-критерий Стьюдента проверить значимость полученного коэффициента корреляции и сделать вывод о тесноте связи между факторами X и Y.
3. Полагая, что взаимосвязь между факторами X и Y может быть описана линейной функцией, записать соответствующее уравнение этой зависимости. Вычислить оценки неизвестных параметров уравнения парной регрессии по методу наименьших квадратов на основе решения системы нормальных уравнений. Проинтерпретировать полученные результаты в терминах решаемой задачи.
4. Проверить значимость всех параметров модели по t-критерию Стьюдента. Для значимых коэффициентов построить доверительные интервалы. Сформулировать выводы.
5. Проверить значимость модели (уравнения регрессии) в целом с помощью F-критерия Фишера. Сформулировать вывод.
6. Построить таблицу дисперсионного анализа.
7. Выбрать прогнозную точку x P в стороне от основного массива данных. Используя уравнение регрессии выполнить точечный прогноз величины Y в точке x P .
8. Рассчитать доверительные интервалы для уравнения регрессии и для результативного признака y P при доверительной вероятности a = 0.95.
9. Изобразить в одной системе координат исходные данные, линию регрессии, точечный прогноз, 95% доверительный интервал.
10. Сделать общие выводы по проделанной работе.
Решение:
1. Исходные данные нанести на координатную плоскость. Сделать предварительное заключение о наличии взаимосвязи между факторами X и Y, о ее характере (положительная или отрицательная) и форме (линейная или нелинейная):
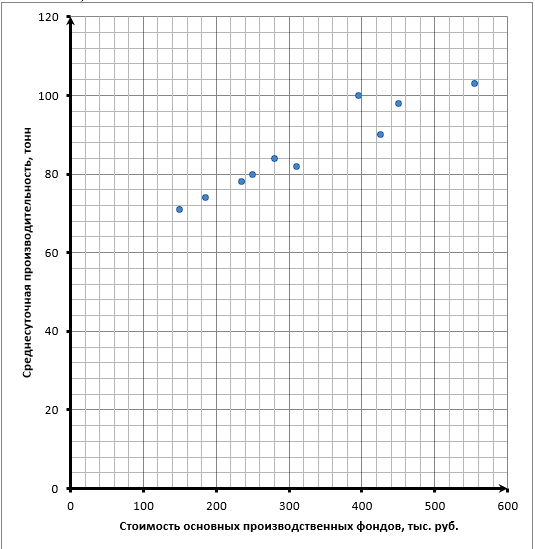
Рис. 1 Поле корреляции
На основании поля корреляции выдвинем гипотезу о том, что связь между всеми возможными значениями х и у, то есть для генеральной совокупности может быть линейна:...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства