Построить уравнение парной линейной регрессии y на х, где Price – зависимая переменная, а в качестве независимой переменной х необходимо выбрать один фактор из нескольких предложенных, имеющий наибольшую взаимосвязь с зависимой переменной.
- Эконометрика
Условие:
1. Построить уравнение парной линейной регрессии y на х, где Price – зависимая переменная, а в качестве независимой переменной х необходимо выбрать один фактор из нескольких предложенных, имеющий наибольшую взаимосвязь с зависимой переменной. Выбор данного фактора необходимо осуществить на основании сравнения величин линейных коэффициентов корреляции.
2. Сформировать расчетную таблицу заданной структуры.

3. Ввести ряды данных в таблицу по столбцам. Рассчитать суммы и средние рядов данных с помощью функций СУММ(…) и СРЗНАЧ(…).
4. Построить корреляционное поле при помощи Мастера диаграмм (тип – Точечная диаграмма) и провести визуальный анализ.
5. Рассчитать параметры линейного выборочного уравнения парной регрессии ŷ=a+bx с использованием формул:
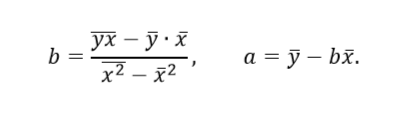
6. Найти значения выборочных дисперсий и СКО x, y по формулам:
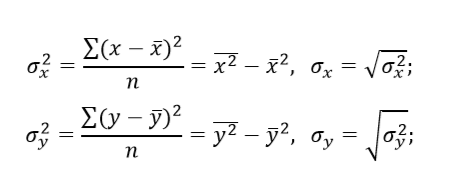
Проверить результат с помощью функций:
ДИСПР(…) и СТАНДОТКЛОНП(…).
7. Рассчитать выборочный коэффициент корреляции с использованием одной из формул:
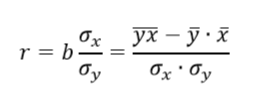
Проверить результат с помощью функции КОРРЕЛ(…).
8. Вычислить средний коэффициент эластичности ![]()
9. Вычислить предсказанные моделью значения y по построенному уравнению регрессии ŷ =a+bx.
10. Вычислить остатки и их квадраты. Остатки вычисляются по формуле e=y-ŷ.
11. Вычислить значения ![]()
12. Рассчитать суммы квадратов отклонений (СумКО), дисперсии и СКО на 1 степень свободы (общая, факторная, остаточная).
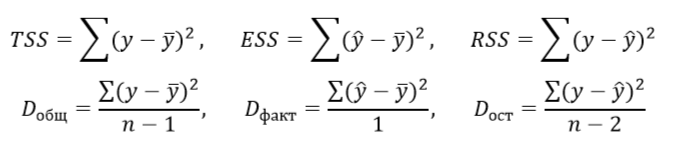
где TSS – общая СумКО (total sum of squares), ESS – факторная СумКО, RSS – остаточная СумКО.
13. Проверить балансовое соотношение для суммы квадратов отклонений:
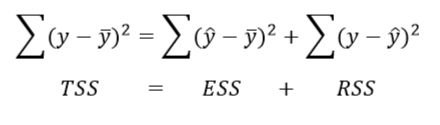
14. Рассчитать коэффициент детерминации R2 и индекс корреляции R c использованием сумм квадратов отклонений:
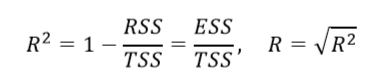
Проверить результат с использованием коэффициента корреляции R2=r2 и с помощью функции КВПИРСОН(…).
15. Рассчитать стандартную ошибку коэффициента регрессии и значение статистики Стьюдента:
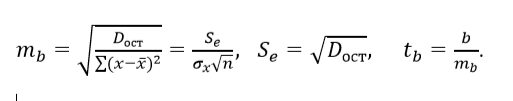
16. Проверить статистическую значимость коэффициента b на уровнях 0,05 и 0,01. При определении табличного значения статистики воспользоваться функцией СТЬЮДРАСПОБР(…). Если |tb|>tтабл(α;n-2), то коэффициент b статистически значимо отличен от нуля.
17. Построить доверительный интервал для коэффициента регрессии на уровне значимости 0,01:
b-mb∙tтабл (α,n-2)≤β≤b+mb∙tтабл (α,n-2)
18. Рассчитать значение статистики Фишера F через факторную и остаточную дисперсии: ![]()
19. Проверить результат вычисления статистики с использованием коэффициента детерминации и статистики Стьюдента для b:
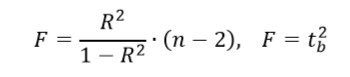
20. Проверить статистическую значимость уравнения в целом на уровне 0,05. Табличное значение F определить через функцию FРАСПОБР(…). Если F>Fтабл (α,1,n-2), то уравнение признается в целом статистически значимым.
21. Проверить качество уравнения по средней относительной ошибки аппроксимации:
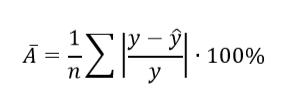
Значение ![]() берется из суммарной ячейки столбца
берется из суммарной ячейки столбца 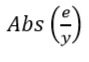 расчетной таблицы.
расчетной таблицы.
22. С помощью инструмента Регрессия Пакета анализа построить линейную регрессию y на x. Найти xp, если прогнозное значение фактора увеличится на 5% от его среднего значения.
23. Подставить прогноз xp в уравнение регрессии y на x и получить прогноз yp.
24. Построить 90% -й интервал прогноза yp:
![]()
a) для среднего прогнозного значения:
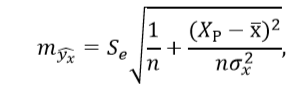
б) для индивидуального прогнозного значения:
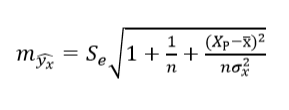
Решение:
1. Для выбора фактора по данным индивидуального варианта задания необходимо построить матрицу линейных коэффициентов корреляции в MS Excel: вкладка Данные Анализ данных инструмент Корреляция (рис.1).
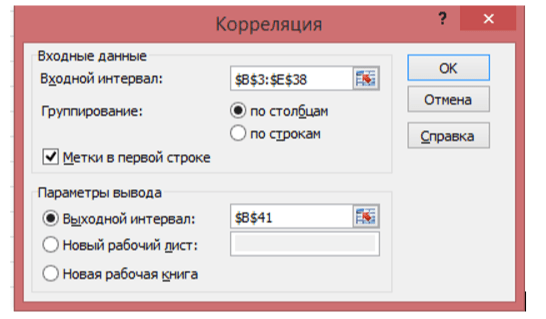
Рис. 1. Окно параметров корреляции с введенными значениями в MS Excel
Далее, нажав на кнопку Ок, получаем следующую матрицу линейных коэффициентов корреляции (рис. 2):
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства