Уравнение движения точки имеет вид, указанный в таблице 1. Пользуясь уравнением, выполнить следующее: 1 определить координату x0 точки в начальный момент времени;
- Физика
Условие:
Уравнение движения точки имеет вид, указанный в таблице 1. Пользуясь уравнением, выполнить следующее:
1) определить координату x0 точки в начальный момент времени;
2) написать формулу зависимости скорости от времени;
3) найти начальную скорость v0 точки;
4) найти ускорение a точки;
5) построить график зависимости координаты от времени x = f(t) и скорости от времени v = f(t) в интервале 0 ≤ t ≤ τ c шагом Δt ;
6) указать характер движения точки.
Таблица 1
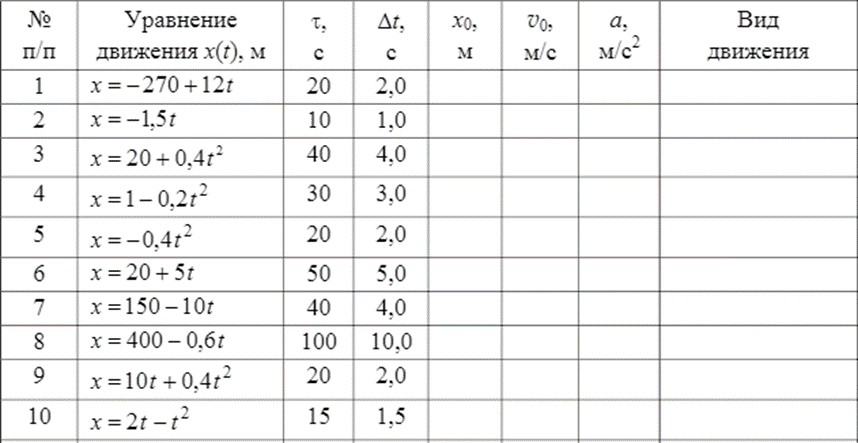
Решение:
Дано: x(t) = 2t - t2 ; t = 0.
Найти: x0 , x = f(t), v0 , a.
Построить график зависимости координаты от времени x = f (t) скорости от времени v = f (t) в интервале 0 t c шагом t.
Зависимость координаты от времени задана выражением:
x(t) = 2t - t2 . (1)
Определим начальную координату тела, полагая, что t0 = 0 .
Подставим значение t0 = 0 в уравнение (1), получим, что
x0 = 0.
Известно, что скорость является первой производной координаты по времени. Продифференцируем выражение (1), получим:
v = dx/dt (2)
v = 2 - 2t. (3)
Определим начальн...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства