Условие задачи
Вычисление координат спутника в земной системе с учетом возмущений от сжатия Земли
Постановка задачи
Если Землю и вращающийся вокруг ее спутник считать материальными точками, то под действием сил взаимного притяжения и при отсутствии других сил (от притяжения небесных тел, сопротивления атмосферы и т.п.) спутник будет двигаться по невозмущенной орбите. Теория такого движения рассматривается в небесной механике как задача двух тел. Невозмущенное движение спутника происходит в соответствии с законами Кеплера по орбите, у которой размеры, форма и ориентировка в пространстве остаются постоянными.
Реальное движение спутника происходит под постоянным воздействием на него различных сил, из которых наибольшее влияние оказывает сжатие Земли. Эти дополнительные к силе притяжения шаровой Земли силы называют возмущающими силами, а происходящие в орбите изменения - возмущениями. Применяемый при изучении возмущенного движения принцип Лагранжа заключается в том, что движение рассматривают происходящим по кеплеровой орбите с постоянно изменяющимися элементами. В каждый момент времени можно определить невозмущенную орбиту, совпадающую с моментальной возмущенной орбитой. Такие орбиты называют оскулирующими в некоторую эпоху t .
Необходимо по элементам орбиты, данным на начальную эпоху t0 , найти элементы оскулирующей орбиты на эпоху t с учетом возмущений от сжатия Земли. По ним предстоит рассчитать прямоугольные координаты x, y, z в небесной (инерциальной) системе, от которых затем перейти к земной системе координат.
Исходные данные
Элементы орбиты: a – большая полуось, e – эксцентриситет, i – наклонение, Ω – долгота восходящего узла, ω – аргумент перигея, M0 – средняя аномалия в эпоху t0.
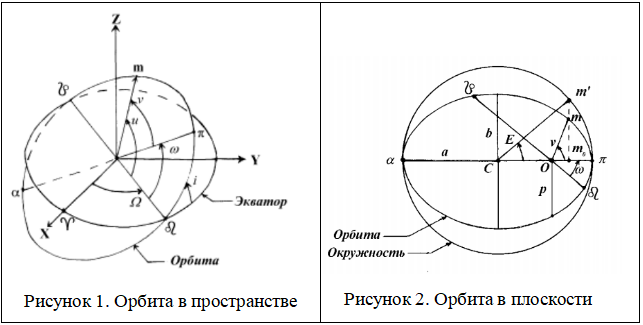
Таблица 1. Элементы оскулирующей орбиты
Таблица 2. Дополнительная информация для вычислений
Числовые данные для решения:
- большая полуось общеземного эллипсоида aE = 6378137 м,
- коэффициент второй зональной гармоники C20=1.08263·10-3,
-геоцентрическая гравитационная постоянная GM = 398600.5 км3с-2 .
Ответ
1. Вычисление момента S2, на который необходимо рассчитать эфемериду спутника, по формуле:
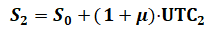
где всемирное время UTC2 и звездное время в Гриническую полночь S0 выбираются из таблицы 2. Коэффициент служит для преобразования единиц среднего солнечного времени в звездное: =0.0027379035.
