Условие:
(Рис. 5.3). К закрытому резервуару, на свободной поверхности которого действует манометрическое давление рм, с правой стороны подсоединен чугунный трубопровод переменного сечения с диаметрами d1и d2. На первом участке длиной l1 установлен вентиль, коэффициент сопротивления которого ζв. Второй участок длиной l2 заканчивается соплом диаметром dс = d1с коэффициентом сопротивления ζс = 0,06 (коэффициент сжатия струи на выходе из сопла ε = 1). С левой стороны находится затопленный конический сходящийся насадок с диаметром выходного сечения dH, истечение из которого происходит при постоянной разности уровней Н и коэффициентом расхода μн, и длиной lн = 5dн. Трубопровод и насадок подсоединены на глубине Н1 температура воды t = + 10°С.
Определить:
Скорость истечения υcи расход Qc, вытекающей из сопла воды.
Расход воды через затопленный насадок QH.
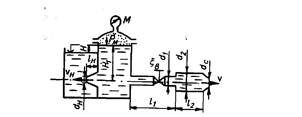
Исходные данные: l1 = 12 м, l2 = 6 м, d1 = 1,2∙10-2 м,
d2 = 2,5∙10-2 м, dн = 1,2∙10-2 м, Н = 2,5 м,
Н1= 8,5 м, рм = 400 кПа, μн = 0,94, ζв = 4,
υс= ? Qс = ? Qн = ?
Решение:
Запишем уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0 (Рис.1 ).
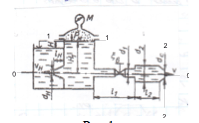
Рис.1.
Уравнение Бернулли в общем виде запишется:
z- высота центра тяжести сечения над плоскостью сравнения 0-0, м;
пьезометрическая высота, м;
