1. Главная
  2. Библиотека
  3. Информатика
  4. Найти вероятность отказа в обслуживании, вероятность обслуживания, интенсивность потока автомашин прошедших ТО, интенсивно...

Найти вероятность отказа в обслуживании, вероятность обслуживания, интенсивность потока автомашин прошедших ТО, интенсивность потока автомашин не прошедших ТО, среднюю длину очереди, коэффициент загрузки СТО и др.

«Найти вероятность отказа в обслуживании, вероятность обслуживания, интенсивность потока автомашин прошедших ТО, интенсивность потока автомашин не прошедших ТО, среднюю длину очереди, коэффициент загрузки СТО и др.»
  • Информатика

Условие:

Станция технического обслуживания (СТО) 

СТО автомашин может одновременно проводить техническое обслуживание (ТО) не более X автомашин. Еще Z автомашин, прибывающих на СТО, могут занять специальную площадку для ожидания ТО. Если на СТО уже (X+Z) автомашин (X на ТО и Z в очереди), то следующая автомашина, прибывшая на СТО, покинет ее без ТО. Входящий поток автомашин — простейший поток событий (ППС) с интенсивностью 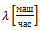, время ТО одной автомашины — случайная величина, распределѐнная по экспоненциальному закону со средним значением 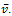. Соответственно интенсивность ТО . 

Найти вероятность отказа в обслуживании Pотк, вероятность обслуживания (прохождения ТО) Робс, интенсивность потока автомашин прошедших ТО λобс, интенсивность потока автомашин не прошедших ТО  λотк, среднюю длину очереди 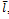, коэффициент загрузки СТО R, среднее число занятых каналов обслуживания СТО 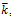, коэффициент загрузки каждого канала обслуживания СТО R1, среднее число автомашин на СТО среднее время ожидания в очереди , среднее время пребывания в СТО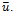

Решение:

Имеем трехканальную СМО с ограниченной длиной очереди (m=2).

Обозначим через Si возможные состояния СМО, где i число машин на СТО. Тогда граф переходов между состояниями имеет вид:

Вычисляем нагрузку на СМО:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я