Условие задачи
Построить множество дизъюнктов для рассуждения. Для этого привести посылки и отрицание заключения к ПНФ, а затем к Сколемовской стандартной форме. Методом резолюции вывести пустой (тождественно ложный) дизъюнкт из исходного множества дизъюнктов, доказав тем самым справедливость рассуждения.
Ни один преподаватель не является невеждой. Некоторые невежды попадают в институт. Следовательно, некоторые люди, попадающие в институт, не являются преподавателями.
Ответ
Докажем рассуждение от противного, построив логическое произведение посылок и отрицания заключения.
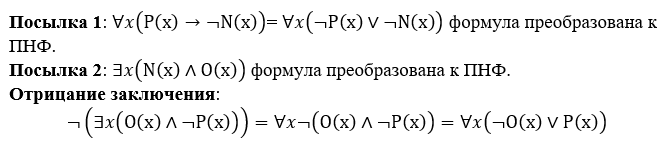
формула преобразована к ПНФ.
Преобразование Сколема и получение множества дизъюнктов.
Посылка 1: при отсутствии кванторов существования совпадает со Сколемовской стандартной формой.
Потяни
