Условие:
Стальному ступенчатому валу, имеющему сплошное круглое поперечное сечение, приложены четыре момента. Левый конец вала жестко закреплен в опоре, а правый конец - свободен и его торец имеет угловые перемещения относительно левого конца.
Требуется:
1) построить эпюру внутренних крутящих моментов по длине вала;
2) при заданном значении допускаемого напряжения на кручение определить
диаметры d1 и d2 вала из условия прочности, полученные значения округлить;
3) построить эпюр углов поворота сечений.
Дано:
Е = 2·105 МПа,
G = 0,4·Е,
a = 1,5м,
b = 1,0 м,
c = 1,7 м,
d = 1,2 м,
T1 = 3,5 кН·м,
T2 =5,6 кН·м,
T3 = 2,0 кН·м, [τ] = 40 МПа.
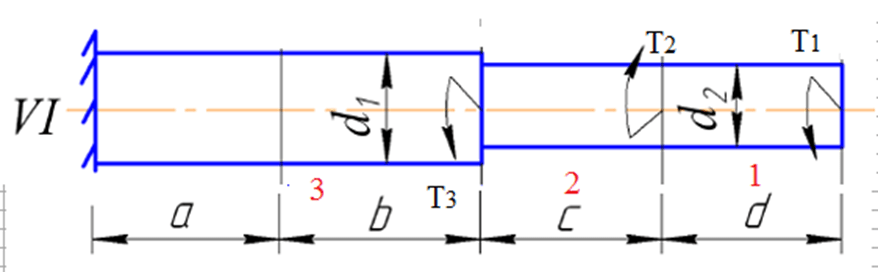
Рисунок 4.1.
Решение:
1) Разобьем вал на участки, на каждом участке проведем сечение, отбросим левую закрепленную часть, а ее действие заменим внутренним скручивающим моментом.
Участок: 1 длина d = 1,2 м;
2 длина c = 1,7 м;
3 длина (а + b) = 2,5 м.
Условие равновесия отсеченной части: Мi кр = 0, отсюда
М1кр = -Т1 = -3,5 кНм,
М2 кр = -Т1 + Т2 = -3,5 + 5,6 = 2,1 кНм,
М3 кр = -Т1 + Т2 - Т3 = 2,1 - 2,0 = 0,1 кНм. Строим эпюр внутренних моментов.
2) Определяем диаметры из условия прочности.
Условие прочности при кручении выражается формулой: max = Мmax /Wp []
где Wp - полярный момент сопротивления
