Найти все корни уравнения f(x)=0 на отрезке [–10, 10]. Варианты уравнений приведены в табл. 4.2. На первом этапе следует отделить корни.

16 августа 2024
Программирование

Условие:

Найти все корни уравнения f(x)=0 на отрезке [–10, 10]. Варианты уравнений приведены в табл. 4.2. На первом этапе следует отделить корни. Для этого нужно вычислить значения функции у=f(x) на отрезке [–10,10] с шагом Н = 0,5 и зафиксировать отрезки [aj, bj], на концах которых функция меняет свой знак. Для каждого варианта нужно построить график функции и таблицу ее значений на отрезке [–10,10] с шагом 0,5. После отделения корней следует уточнить корни одним из следующих методов с точностью ε= 0,001:

половинного деления,
секущих,
хорд,
Ньютона,
прослой итерации.
модифицированный метод Ньютона,
Эйткена-Стеффенсона,
квадратичной интерполяции-экстраполяции,
поразрядного уточнения.

На каждой итерации в одну строку печатать k, x_k, f(_xk). Критерием окончания итерационного процесса может быть:

|f(_xk)| <ε;
|x_k – x_k–1| < ε, при |x_k|<1;

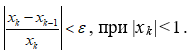
Варианты индивидуальных заданий приведены в табл. 4.3.

Таблица 4.2

Данные к заданию 2

Вариант	Уравнение
18	x log₃ \|x + 1\|

Таблица 4.3

Варианты индивидуальных заданий к заданию 2

Вариант	18
Метод	9
Критерий	2

Решение:

Требуется найти все корни уравнения x log₃ |x + 1| = 1 на отрезке[10, 10]. На первом этапе отделим корни. Для этого вычислим значения функции f (x) = x log₃ |x + 1| - 1 на отрезке [10,10] с шагом Н = 0,5:

x f (x) x f (x) -10.0 -21.00 0.0 -1.00 -9.5 -19.51 0.5 -0.82 -9.0 -18.04 1.0 -0.37 -8.5 -16.59 1.5 0.25 -8.0 -15.17 2.0 1.00 -7.5 -13.78 2.5 1.85 -7.0 -12.42 3.0 2.79 -6.5 -11.09 3.5 3.79 -6.0 -9.79 4.0 4.86 -5.5 -8.53 4.5 5.98 -5.0 -7.31 5.0 7.15 -4.5 -6.13 5.5 8.37 -4.0 -5.00 6.0 9.63 -3.5 -3.92 6.5 10.92 -3.0 -2.89 7.0 12.25 -2.5 -1.92 7.5 13.61 -2.0 -...