1. Разработать программу на языке MATLAB (Scilab), реализующую разложение матрицы указанным методом (в соответствии с вариантом)
- LU разложение с частичным выбором ведущего элемента.
2. Применить программу для решения заданной системы линейных алгебраических уравнений.
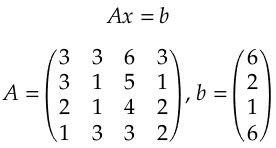
3. В случае невозможности разложения матрицы указанным методом необходимо подробно разъяснить причину и предложить вариант изменения условий таким образом, чтобы СЛАУ можно было решить заданным методом.
1) cоставляем функцию в MATLAB для LU разложения матрицы:
function [L,U,P]=lufunc(A)
k = size(A);
L = zeros(k);%нижняя треугольная
U = eye(k);%верхняя треугольная
P = eye(k);%матрица перестановок
%определяем ведущий элемент
j=1;
imax=j;
smax=abs(A(j,j));
for i = j+1:k%сравниваем с другими строками
if abs(A(i,j))smax
smax=A(i,j);
imax=i;%получили номер строки с главным элементом
end
end
if imax~=j
%меняем строки в матрице
stemp=A(j,:); A(j,:)=A(imax,:);A(imax,:)=stemp;
%записываем матрицу перестановок
stemp=P(j,:); P(j,:)=P(imax,:);P(imax,:)=stemp;
end
%Вычислим поддиагональные элементы:
for i = 2:k
L(i,j)=A(i,j...
Не нашел нужную задачу?