Условие задачи
· Составить программу для решения системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента, нахождения определителя матрицы системы и обратной матрицы. Исходные данные – матрица системы уравнений и столбец свободных членов должны читаться из файла, а результаты расчетов помещаться в файл. В случае, когда матрица системы вырождена, выдать об этом сообщение. В противном случае вывести решение системы, невязки, величину определителя, обратную матрицу. Подобрать тестовые примеры, предусматривающие различные ситуации (матрица вырожденная, невырожденная) и провести вычисления.
· Найти число обусловленности матрицы системы в некоторой, выбранной Вами норме для Ваших тестовых примеров.
· Отключить в программе процедуру выбора главного элемента и найти решение системы (предполагается, что вещественные переменные имеют тип float)
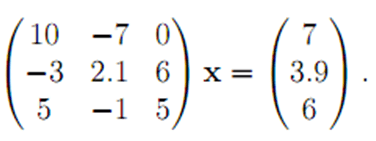
Объяснить результат.
• Решить систему
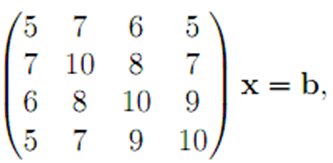
выбирая b равным
Пояснить полученные результаты.
Ответ
2.1. Решение системы линейных алгебраических уравнений
Метод Гаусса это метод последовательного исключения неизвестных. Суть его состоит в преобразовании (2.1) к системе с треугольной матрицей, из которой затем последовательно (обратным ходом) получаются значения всех неизвестных. Рассмотрим одну из вычислительных схем, которая называется схемой единственного деления.
Пусть a11 0 (ведущий элемент).
Этап 1
Приводим систему к треугольному виду.
Шаг 1:
