1. Осуществите проверку первичной информации по факторному признаку на однородность и нормальность распределения. Исключите резко выделяющиеся единицы из массива первичной информации.
- Статистика
Условие:
1. Осуществите проверку первичной информации по факторному признаку на однородность и нормальность распределения. Исключите резко выделяющиеся единицы из массива первичной информации.
2. Постройте ряд распределения отобранных единиц по факторному признаку. Число групп определите по формуле Стерджесса. По построенному ряду распределения рассчитайте показатели:
· центра распределения (среднюю арифметическую, моду, медиану);
· степени вариации (размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент осцилляции, линейный коэффициент вариации, коэффициент вариации, относительный показатель квартильной вариации);
· дифференциации (коэффициент фондовой дифференциации, коэффициент децильной дифференциации);
· концентрации (кривая Лоренца, коэффициент Джини);
· формы распределения (асимметрия, эксцесс).
Сформулируйте выводы.
3. Полагая, что данные по 48 единицам представляют собой 10%-ю простую случайную выборку, с вероятностью 0,9973 определите доверительный интервал, в котором будет находиться средняя величина факторного признака для генеральной совокупности.
4. Проанализируйте зависимость результативного признака от факторного. Анализ выполните в следующей последовательности:
· с помощью групповой таблицы и эмпирической линии регрессии установите факт наличия корреляционной связи;
· проверьте правило сложения дисперсий. Сформулируйте вывод о степени влияния факторного признака на величину результативного с помощью эмпирического корреляционного отношения.
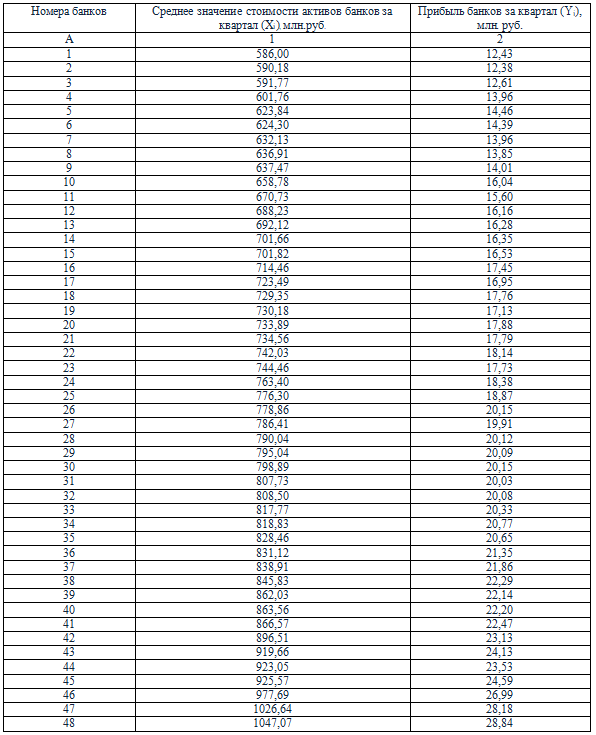
Решение:
1) Осуществите проверку первичной информации по факторному признаку на однородность и нормальность распределения. Исключите резко выделяющиеся единицы из массива первичной информации.
Первичная информация проверяется на однородность по признаку-фактору с помощью коэффициента вариации. Для этого определим среднее значение стоимости активов банков за квартал:
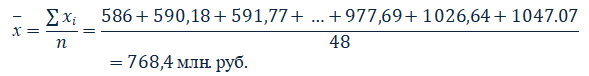
Результаты расчетов среднего квадратическо...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства