Даны значения механической скорости проходки на ста скважинах при одном и том же числе израсходованных долот: 1. Построить интервальный вариационный ряд. Гистограмму.

Даны значения механической скорости проходки на ста скважинах при одном и том же числе израсходованных долот:

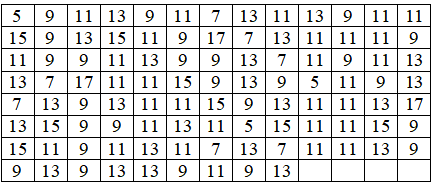
1. Построить интервальный вариационный ряд. Гистограмму.

2. Перейти от интервального вариационного ряда к дискретному, заменив частичные интервалы их серединами. Построить полигон, кумуляту частот, частостей.

3. Найти эмпирическую функцию распределения.

4. Найти числовые характеристики выборки: моду, медиану, выборочное среднее, выборочное среднее квадратическое отклонение, коэффициент вариации, асимметрию, эксцесс.

5. Сделать предварительный выбор закона распределения случайной величины.

6. Проверить согласованность эмпирической и теоретической функций распределения выбранного закона распределения с помощью критериев согласия χ²-Пирсона, Колмогорова при уровне значимости α=0,05.

7. Определить интервальные оценки для генеральной средней, генерального среднего квадратического отклонения нормального закона распределения с надёжностью γ=0,95.