1. Главная
  2. Библиотека
  3. Статистика
  4. Сделайте выводы, укажите вид таблицы и вид группировки. Постройте гистограмму.  Результаты группировки оформите в таблице....

Сделайте выводы, укажите вид таблицы и вид группировки. Постройте гистограмму.  Результаты группировки оформите в таблице.

«Сделайте выводы, укажите вид таблицы и вид группировки. Постройте гистограмму.  Результаты группировки оформите в таблице.»
  • Статистика

Условие:

За отчетный период известны данные по 20 магазинам:

№ магазина Торговая      площадь,кв.м Товарооборот, млн. руб. №  магазина Торговая      площадь,кв.м Товарооборот, млн. руб.
1 12 2 11 15 22
2 30 8 12 45 43
3 16 5 13 25 35
4 22 12 14 20 32
5 34 20 15 37 48
6 10 2 16 44 53
7 15 4 17 39 43
8 28 7 18 19 12
9 38 17 19 23 20
10 35 17 20 41 45

Для выявления зависимости между товарооборотом и размером торговой   площади магазинов произведите группировку магазинов по размеру торговой площади. Количество групп с равными интервалами определите по формуле Стерджесса. Полученные группы охарактеризуйте числом магазинов, размером торговой площади всего и в среднем на один магазин, а также объемом товарооборота всего и в среднем на один магазин. Результаты группировки оформите в таблице. Сделайте выводы, укажите вид таблицы и вид группировки. Постройте гистограмму. 

Для решения задачи используйте шаблоны таблиц:

Таблица – Группировка магазинов по размеру торговой площади

№ группы Группы магазинов по размеру торговой площади, кв. м Число магазинов в абсолютном выражении Число магазинов в относительных единицах, %
       
       
Итого   100

Таблица – Группировка магазинов по размеру торговой площади (рабочая таблица)

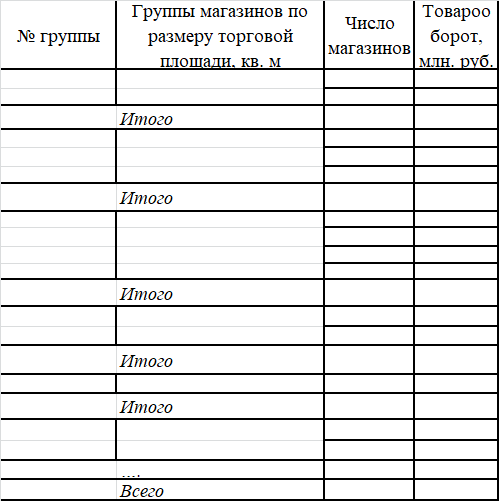
Таблица – Группировка магазинов по размеру торговой площади (аналитическая таблица)

Решение:

Количество групп определим по формуле Стерджесса: k=1+3,322lgN,

N число единиц совокупности.

k=1+3,322lg (20) =5,322=5 групп.

Ширину интервала определим по формуле: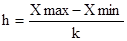

где хmax максимальное значение признака;

хmin минимальное значение признака;

k количество групп.

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я