Составить интервальный статистический ряд распределения относительных частот и построить гистограмму и полигон относительных частот.
- Статистика
Условие:
По заданному варианту выборочной совокупности независимых и равноточных измерений случайной величины Х(СВХ) (предварительно удалив резко выделяющиеся наблюдения):
1. Составить интервальный статистический ряд распределения относительных частот и построить гистограмму и полигон относительных частот.
2. Вычислить точечные оценки для математического ожидания, среднеквадратического отклонения, коэффициента асимметрии.
3. Найти эмпирическую функцию распределения и построить ее график.
4. Исходя из общих представлений о механизме образования СВ X, а также повиду гистограммы и полигона относительных частот и вычаленным числовым характеристикам, выдвинуть гипотезу о виде распределения СВ X, записать плотность распределения вероятностей и функцию распределения для выдвинутого гипотетического закона, заменяя параметры закона вычисленными для них оценками.
5. По критерию согласия χ 2 Пирсона проверить соответствие выборочного распределения гипотетическому закону для уровня значимости q=0,05.
6. Вычислить интервальные оценки для математического ожидания m и среднеквадратического отклонения, соответствующие доверительным вероятностям 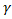 =0,95 и
=0,95 и 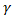 =0,99.
=0,99.
В таблице приведены данные об убойном весе 100 бычков.
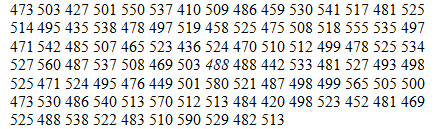
Решение:
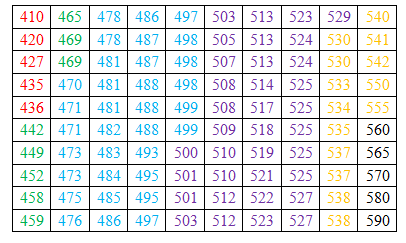
1. Составим интервальный статистический ряд распределения относительных частот и построим гистограмму и полигон относительных частот.
При выборе числа kчастичных интервалов руководствуются обычно следующими правилами:
- при n 200 выбираем от 10 до 20 интервалов; при n =100 лучше брать пять-семь интервалов;
- выбранные k интервалов должны охватывать всю область данных;
- интервалы не должны перекрыв...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства