Условие:
Однородная горизонтальная платформа (прямоугольная со сторонами R и 2R, где R=1,2 м) массой 𝑚1=24 кг вращается с угловой скоростью 𝜔0=10 рад/с вокруг вертикальной оси z, отстоящей от центра масс С платформы на расстоянии ОС=b=1,2 м; размеры прямоугольной платформы показаны на рис. 2 (вид сверху).
В момент времени 𝑡0 = 0 по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой 𝑚2 = 8 кг по закону s = F(t) = 0,6·cos2t, где s выражено в метрах, t – в секундах. Одновременно на платформу, изображенную на рис. 1, начинает действовать пара сил с моментом М = 8 Н·м.
Определить для платформы зависимость 𝜔 = 𝑓(𝑡), т.е. угловую скорость платформы, как функцию времени; для платформы в момент времени 𝑡1=1 с.
Форма желоба на рис. 1 прямолинейная (желоб KE). Груз D показан в положении, при котором s>0 (когда s<0, груз находится по другую сторону от точки А).
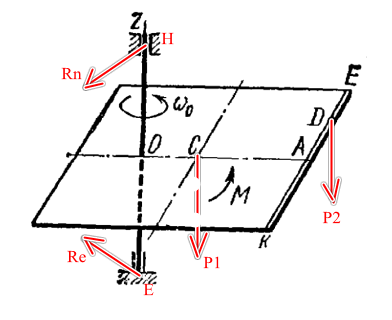
Рисунок 1.
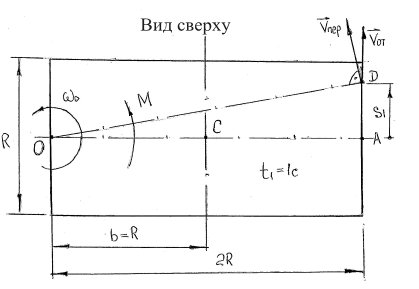
Рисунок 2
.
Решение:
Математическое выражение теоремы об изменении кинетического момента, имеет вид:
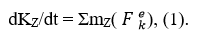
На систему действуют следующие внешние силы:
силы тяжести Р1 и Р2 , соответственно платформы и груза D и которые параллельны оси вращения Z и следовательно не создают моментов относительно этой оси, не создают моментов и реакции опор RE и RН, т.к. пересекают эту ось, следовательно:
