По заданным уравнениям движения точки М в декартовых координатах x = f1(t), y = f2(t) найти: 1) уравнение траектории точки; 2) скорость и ускорение точки в произвольный момент времени t, а также в момент времени t = t1;
- Теоретическая механика
Условие:
По заданным уравнениям движения точки М в декартовых координатах x = f1(t), y = f2(t) найти:
1) уравнение траектории точки;
2) скорость и ускорение точки в произвольный момент времени t, а также в момент времени t = t1;
3) касательное и нормальное ускорения точки в момент времени t1;
4) радиус кривизны траектории в момент времени t = t1.
Кроме того, построить, выбрав соответствующие масштабы для длин, скоростей и ускорений:
1) траекторию точки;
2) положение точки на траектории в момент временя t = t1;
3) скорость и ускорение точки, а также касательное и нормальное ускорения для момента времени t = t1.
Уравнения движения точки и момент времени t = t1
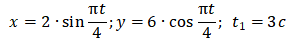
величины коэффициентов а = 2; b = 6
Решение:
Для определения уравнения траектории точки исключим из заданных уравнений движения время t.
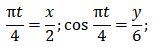
Воспользуемся известным соотношением
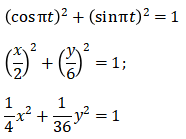
Это уравнение эллипса. Центр эллипса расположен в точке (0; 0).
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства