Условие:
Для данной матрицы:
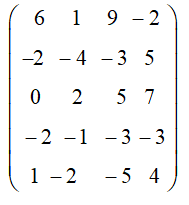
1. упростить матрицу, исключив из неё доминируемые строки, соответствующие заведомо невыгодным стратегиям активного игрока;
2. восстановить пропущенную вероятность одной из гипотез о «поведении природы»;
3. выявить оптимальную стратегию активного игрока по математическому ожиданию прибыли;
4. выявить оптимальные стратегии активного игрока, применяя
4.1. оптимистический критерий
4.2. пессимистический (Вальде) критерий,
4.3. критерий Гурвица (при γ = 0,3),
4.4. критерий Сэвиджа.
Решение:
1) Первый игрок имеет пять стратегий, а второй, природа, характеризуется четырьмя возможными гипотезами. Известны вероятности реализаций первых трех гипотез. Введем обозначения стратегий активного игрока - получателя выгоды и природы

Сравним строки данной платежной матрицы для выявления заведомо невыгодных игроку стратегий. Составим матрицу разностей элементов строк, соответствующим стратегиям
