Условие:
Два баскетболиста поочередно забрасывают мяч в корзину до тех пор, пока один из них не попадает. Каждый имеет 2 броска.
Определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайного числа бросков, производимым каждым из баскетболистов, если вероятность попадания для первого равна 0,4, а для второго – 0,6. Построить график функции распределения. Найти вероятность того, что каждый из баскетболистов бросит мяч более 1 раза.
Решение:
Составим закон распределения случайной величины X число бросков, которые совершит первый баскетболист.
Случайная величина может принимать значения 1 и 2, определим соответствующие вероятности:
- x=1 (первый баскетболист попал или же первый промахнулся, а второй попал):
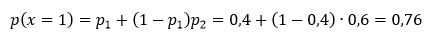
- x=2 (оба баскетболиста промахнулись при первом броске):
