Условие задачи
Используя логико-вероятностные методы расчета надежности, необходимо определить вероятность безотказной работы P и вероятность отказа Q системы в соответствии с вариантом задания, при условии, что вероятность безотказной работы i-го элемента равна pi, а вероятность отказа – qi.
Структурная схема:
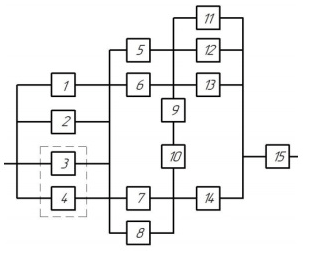
Вероятности отказа и безотказной работы элементов:
q1=0,08;
p2=p3=⋯=p11=0,92;
p12=0,95;
q13=q14=0,05;
q15=0,04.
Для соединения «m из n» должен быть использован комбинаторный метод расчета, для соединения «мостик» - метод логических схем.
Ответ
Определим вероятность безотказной работы элемента 1:
p1=1-q1=0,92.
Для элементов 13 и 14:
p13=p14=1-q13=0,95.
Для элемента 15:
p15=1-q15=0,96.
Рассмотрим элементы 1, 2, 3, 4. Они образуют систему 2 из 4 - это значит, что система работоспособна тогда, когда в ней работают любые два элемента из четырех. Обозначим это соединение как квазиэлемент A. Применим комбинаторный метод расчета вероятности безотказной работы:









