Исходными данными при интерполяции является таблица значений функции. Для выполнения сформулированного ниже задания к лабораторной работе таблицу получить путем аналитического определения функции у = f(x) и задания массива значений аргумента.

Исходными данными при интерполяции является таблица значений функции. Для выполнения сформулированного ниже задания к лабораторной работе таблицу получить путем аналитического определения функции у = f(x) и задания массива значений аргумента.

·         Составить программу для построения интерполяционного многочлена Лагранжа (Ньютона) и кубического интерполяционного сплайна дефекта 1. Используя таблицу значений функции, построить интерполяционный многочлен и сплайн, после чего нарисовать графики функции у = f(x), интерполяционного многочлена и сплайна. Обратите внимание, что при построении графиков число точек, в которых вычисляются функции должно быть много больше, чем число узлов интерполяции.

·         Анализируя графики, исследовать, путем проведения вычислительных экспериментов, влияние количества и расположения узлов интерполирования, участков интерполирования на погрешность интерполирования. Сравнить результаты интерполирования многочленами и сплайнами для различного вида функций. В качестве функций, для которых проводится анализ, помимо придуманных Вами функций рекомендуется рассмотреть у = |х| при |х| ≤ 1,   при \х\ ≤ 4, у = sinх при |х| ≤p.

·         Экспериментально исследовать чувствительность сплайна к изменению таблицы значений функции. Для этого задать таблицу значений функции, построить по этой таблице сплайн, нарисовать его график, после чего изменить значения в одной из точек таблицы и посмотреть как изменится график сплайна для новой таблицы.

Пусть задан набор точек на плоскости (x_i,y_i), i = 0,1,..., n, которые лежат на некоторой плоской кривой. Предполагается, что точки занумерованы в порядке следования вдоль кривой. Кривая может иметь произвольную форму, например, быть замкнутой, с самопересечениями, поэтому се удобнее задать параметрически, то есть в виде х = x(t), у = y(t). Постройте по заданному набору точек кривую, используя сплайн-интерполяцию для нахождения функций х = x(t), у = y(t). Проанализируйте влияние метода ввода параметра на форму интерполирующей кривой. 

·         Приведем два примеры ввода параметра.

1) (i,x_i), (i, y_i) есть в i-ой точке значение параметра t_i равно i.

2) Пусть 

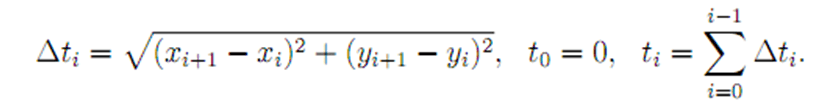
Вы можете придумать еще один-два способа задания параметра. Сравните кривые, полученные при различном способе параметризации.