Условие задачи
Из 500 рабочих, обслуживающих цех производства окиси этилена, было отобрано 100 человек для контрольной проверки коэффициента использования рабочего времени в отчётном году по сравнению с предыдущим.
Были получены следующие данные:
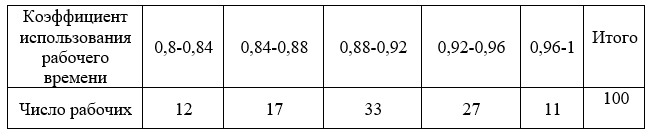
1. Используя критерий 𝜒2 Пирсона, при уровне значимости проверить гипотезу о том, что случайная величина Х – средний коэффициент использования рабочего времени распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
2. Найти:
а) вероятность того, что средний коэффициент использования рабочего времени в отчётном году отличается от идеального среднего коэффициента не более чем на 0,01 (по абсолютной величине);
б) границы, в которых с вероятностью 0,9606 заключен средний коэффициент использования рабочего времени одного рабочего этого цеха;
в) каким должен быть объём выборки, чтобы с вероятностью 0,7373 можно было утверждать, что доля рабочих в цехе, коэффициент использования рабочего времени которых будет менее 0,88, отличалась от доли таких рабочих в выборке не более чем на 0,02 (по абсолютной величине)?
Ответ
1. Найдем выборочную среднюю и средне квадратическое отклонение.
Обозначим 𝑥𝑖 середины интервалов величины коэффициента использования рабочего времени.
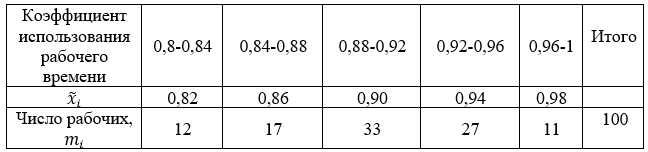
Вычислим средний коэффициент использования рабочего времени, то есть выборочную среднюю по формуле
