Команда состоит из двух стрелков. Числа очков, выбиваемых каждым из них при одном выстреле, являются случайными величинами Х1 и Х2 , которые характеризуются следующими законами распределения:
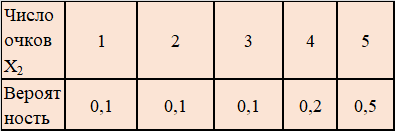
Результаты стрельбы одного стрелка не влияют на результаты стрельбы второго. Составить закон распределения числа очков, выбиваемых данной командой, если стрелки сделают по одному выстрелу.
Если стрелки сделали по одному выстрелу, то их команда наберет число очков, равное сумме очков 1-го и 2-го стрелка. При этом если 1-й стрелок выбил 3 очка, а 2-й одно очко, то сумма составит 3+1=4 очка, если 2-й выбьет 2 очка, то сумма составит 3+2=5 очков, и так далее. Таким образом, возможные суммы: 3+1, 3+2, 3+3, 3+4, 3+5, 4+1, 4+2, 4+3, 4+4, 4+5, 5+1, 5+2, 5+3, 5+4, 5+5.
У нас Х1 результат 1-го стрелка, а Х2 - результат 2-го стрелка, тогда в сумме они наберут Х = Х1 + Х2 очков. Это искомая случайная вели...