Математическое ожидание нормально распределенной случайной величины равно m, ее среднее квадратичное отклонение σ = l - 3. Выполните следующие задания: 1) напишите формулу функции плотности распределения вероятности и схематично
«Математическое ожидание нормально распределенной случайной величины равно m, ее среднее квадратичное отклонение σ = l - 3. Выполните следующие задания: 1) напишите формулу функции плотности распределения вероятности и схематично»
- Теория вероятностей
Условие:
Математическое ожидание нормально распределенной случайной величины равно m, ее среднее квадратичное отклонение σ = l - 3.
Выполните следующие задания:
1) напишите формулу функции плотности распределения вероятности и схематично постройте ее график;
2) найдите вероятность того, что X примет значения из интервала (α,β), где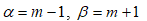 
l =12 m =9
Решение:
Формула плотности заданного нормального распределения с параметрами
а = 9, = l - 3 = 12 -3 = 9.
В общем случае имеет вид:
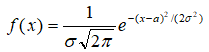
Или в нашем случае:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э