Условие задачи
На отрезок длины l = 13 наугад бросаются две точки. Рассматриваются события:
A = {расстояние между точками не превосходит 4};
B = {наибольшее расстояние точек от начала отрезка заключено в пределах от 3,25 до 6,5};
C = {сумма расстояний точек до начала отрезка меньше либо равно 4,875}.
1. Выбрать соответствующее множество в качестве пространства элементарных исходов рассматриваемого испытания и с помощью его элементов описать события А, В, С.
2. Проверить попарную несовместимость событий А, В, С.
3. Проверить образуют ли события А, В, C полную группу событий.
4. Используя классическое или геометрическое определение вероятности, найти вероятности событий А, В, С.
5. Используя теоремы сложения и умножения найти
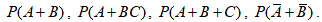
6. Проверить парную и взаимную независимость событий А, В, С.
Ответ
1. Возможно бесконечное множество исходов от 0 (точки совпадают) до l (точки находятся на разных концах отрезка).
Тогда в качестве пространства элементарных исходов можем выбрать множество этих исходов: 
расстояние точек от начала отрезка.
Опишем события A, B, C в элементарных исходах:
Представим возможные варианты событие A на графике:
