1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. На складе имеются две партии пряжи. Первая партия содержит 30%, а вторая — 20% пряжи второго сорта; остальная пряжа в обеи...

На складе имеются две партии пряжи. Первая партия содержит 30%, а вторая — 20% пряжи второго сорта; остальная пряжа в обеих партиях первого сорта. 1) Определить, в пряже какой партии окажется большим

«На складе имеются две партии пряжи. Первая партия содержит 30%, а вторая — 20% пряжи второго сорта; остальная пряжа в обеих партиях первого сорта. 1) Определить, в пряже какой партии окажется большим»
  • Теория вероятностей

Условие:

На складе имеются две партии пряжи. Первая партия содержит 30%, а вторая — 20% пряжи второго сорта; остальная пряжа в обеих партиях первого сорта.

1) Определить, в пряже какой партии окажется большим наиболее вероятное число мотков пряжи первого сорта, если для контроля качества пряжи взяли 40 мотков из первой партии и 30 — из второй.

2) Сколько нужно взять мотков пряжи из первой партии, чтобы наиболее вероятное число мотков пряжи первого сорта в этой партии оказалось равным 5? Найти вероятность этого события.

Решение:

1) Наиболее вероятное (наивероятнейшее) число m0 наступлений события A в n испытаниях определяется неравенством:

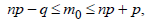
где р = р(А); q =1- p.

В условиях нашей задачи A моток пряжи первого сорта. Для первой партии:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я