Условие:
Найти распределение случайной величины Y, детерминированно связанной со случайной величиной Х функцией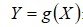 
. Случайная величина X имеет распределение
X~uniform (0, 1).
Таблица 1 –Описание функции
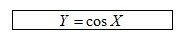
Этапы решения:
1) записать дифференциальную и интегральную функции распределения случайной величины X. Построить графики этих функций;
2) определить характер изменения (монотонность) функции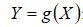 
в интервале изменения случайной величины X. Построить графикфункции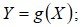 
3) записать формулы, связывающие функции распределения случайной величины Y с распределением случайной величины X;
4) найти обратную функцию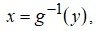 
построить ее график
5) найти дифференциальную и интегральную функции распределения случайной величины Y. Построить графики этих функций.
Решение:
1) Плотность (дифферециальная функция распределения) равномерно распределенной на интервале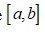 
величины записывается в виде
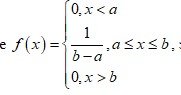, значит,