1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Найти закон распределения, математическое ожидание и дисперсию числа заготовок, оставшихся при изготовлении одной стандарт...

Найти закон распределения, математическое ожидание и дисперсию числа заготовок, оставшихся при изготовлении одной стандартной детали. Построить функцию распределения. Определить вероятность того, что число оставшихся заготовок не менее двух.

«Найти закон распределения, математическое ожидание и дисперсию числа заготовок, оставшихся при изготовлении одной стандартной детали. Построить функцию распределения. Определить вероятность того, что число оставшихся заготовок не менее двух.»
  • Теория вероятностей

Условие:

   Имеется 3 заготовки для одной и той же детали. Вероятность изготовления стандартной детали из каждой заготовки равна 0,2. Найти закон распределения, математическое ожидание и дисперсию числа заготовок, оставшихся при изготовлении одной стандартной детали. Построить функцию распределения. Определить вероятность того, что число оставшихся заготовок не менее двух.

Решение:

Очевидно, что множество возможных значений рассматриваемой СВ Х состоит из четырех элементов Ωx = {0; 1; 2}.

Найдем соответствующие вероятности по теореме умножения для независимых событий и теореме сложения для несовместных событий:

Р(х1=0)=0,8*0,8*0,2+0,8*0,8*0,8=0,64

Р(х2=1)=0,8*0,2=0,16

Р(х3=2)=0,2

Получаем следующий ряд распределения:

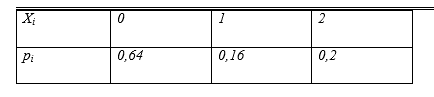
Контроль: 0,64+0,16+0,2=1.

Находим математическое ожидание:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я