Условие задачи
При обследовании N = 2500 предприятий города по издержкам обращения (тыс. руб.), полученным в отчетном периоде, по схеме собственно-случайной выборки было отобрано 100 предприятий. Полученные данные представлены в группированном виде интервалами объема издержек обращения xi и количеством ni предприятий, попавших в i-ый интервал:
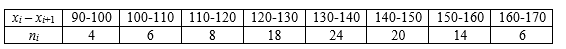
Среднее значение признака в выборочной совокупности равно 134,8 тыс. руб.
Дисперсия 297,96
Среднеквадратичное отклонение равно: 17,262 тыс. руб.
Исправленная выборочная дисперсия: 300,97
Исправленное выборочное среднеквадратичное отклонение: 17,348
Определить, предполагая, что показатели издержек обращения распределено нормально:
1) вероятность того, что средние издержки обращения всех предприятий города отличаются от средних выборочных не более, чем на Δ = 1 тыс. руб. (по абсолютной величине);
2) границы, в которых с вероятностью y1 = 0,95 заключены средние издержки обращения всех предприятий города;
3) долю предприятий, имеющих издержки обращения 140 тыс. руб. и выше, гарантируя результат с вероятностью y2 = 0,99.
Ответ
Поскольку объем выборки n = 100, а генеральной совокупности N = 2500, то имеем n/N =0,04 или 4% выборку.
1) Вероятность того, что средние издержки обращения всех предприятий города отличаются от средних выборочных не более, чем на = 1 тыс. руб. (по абсолютной величине).
Используем формулу
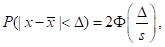
где x̅ = 134,8 выборочное среднее,
s = 17,348 среднеквадратичное отклонение.
Выполним подстановку этих значений ...
