1. Главная
  2. Библиотека
  3. Теория вероятностей
  4. Пусть 1, 2, 5, 4, 5, 4, 5, 4, 5, 11 – выборка из совокупности с теоретическим распределением Пуассона: P(x=k)=λ^k/k! e^(-λ...

Пусть 1, 2, 5, 4, 5, 4, 5, 4, 5, 11 – выборка из совокупности с теоретическим распределением Пуассона: P(x=k)=λ^k/k! e^(-λ),k=0,1,… Построить и вычислить оценку максимального правдоподобия для параметра λ.

«Пусть 1, 2, 5, 4, 5, 4, 5, 4, 5, 11 – выборка из совокупности с теоретическим распределением Пуассона: P(x=k)=λ^k/k! e^(-λ),k=0,1,… Построить и вычислить оценку максимального правдоподобия для параметра λ.»
  • Теория вероятностей

Условие:

Пусть 1, 2, 5, 4, 5, 4, 5, 4, 5, 11 – выборка из совокупности с теоретическим распределением Пуассона:

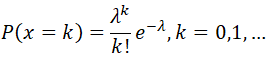
Построить и вычислить оценку максимального правдоподобия для параметра λ.

Решение:

В основе метода лежит функция правдоподобия, имеющая вид:

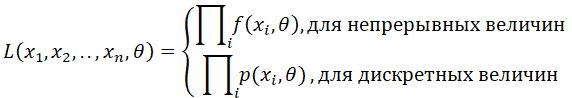
Оценки по методу правдоподобия получаются из необходимого условия экстремума функции (т.е. все частные производные в точке равны нулю). Для случайной величины с заданным распределением:

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я