Размер обработанных на некотором станке деталей может быть рассмотрен как случайная величина Х, распределенная по нормальному закону. Для контроля качества деталей было произведено 50 измерений.
- Теория вероятностей
Условие:
Размер обработанных на некотором станке деталей может быть рассмотрен как случайная величина Х, распределенная по нормальному закону. Для контроля качества деталей было произведено 50 измерений.
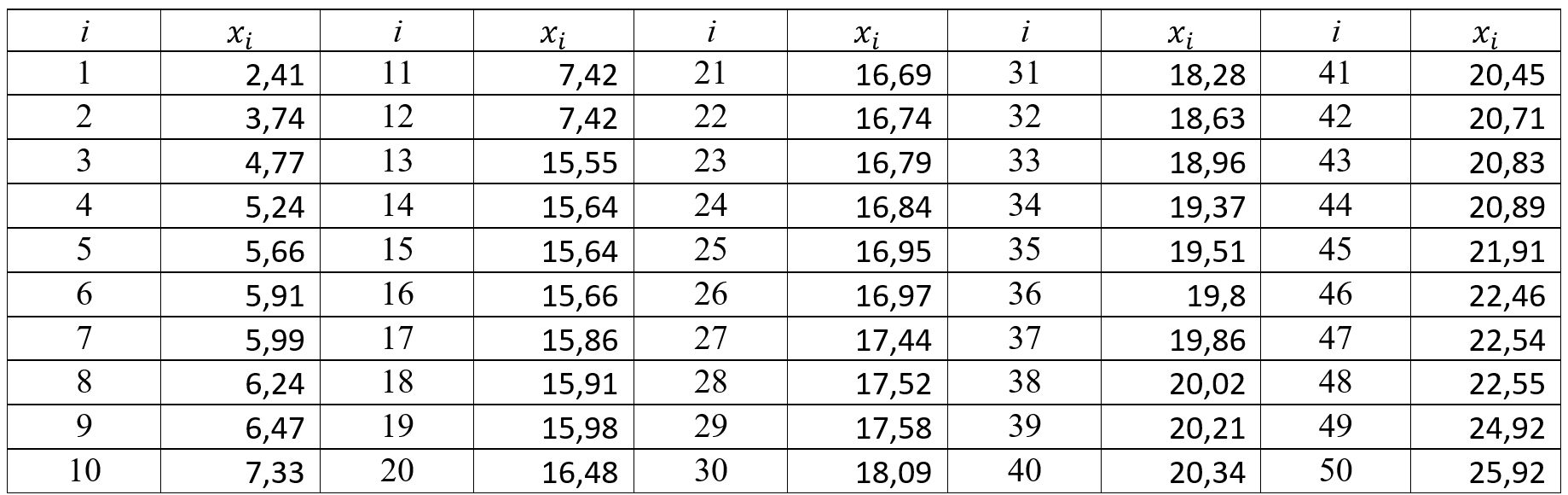
1.1 Провести группировку данных, разбив варианты на 8 интервалов.
1.2 Для сгруппированного ряда построить гистограмму частот.
2.1 Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х.
2.2 Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95.
3.1 Проектный размер детали должен быть равен а=19. При уровне значимости a=0,05 проверить утверждение производителя о совпадении размера произведенных деталей с проектным размером.
3.2. При уровне значимости α=0,05 проверить, является ли статистически обоснованным утверждение производителя о равенстве среднеквадратического отклонения размера детали заданному значению σ0=3.
4.1 Была исследована зависимость случайной величины Y (срок службы произведенных деталей) от величины Х (размер детали). В результате проведения 10 измерений были получены следующие результаты.
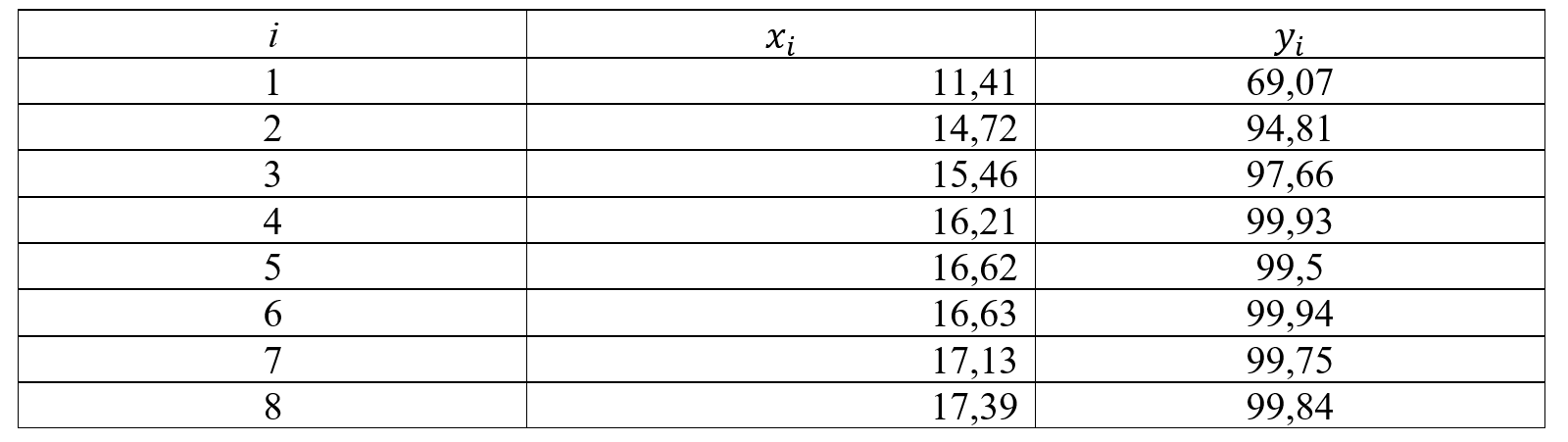
По этим данным построить диаграмму рассеяния.
4.1 Построить линейное уравнение регрессии.
4.2 Построить параболическое уравнение регрессии.
4.3 Для линейной модели проверить адекватность по F-критерию.
4.4 По модели с наименьшей остаточной дисперсией вычислить прогнозируемое значение y* при заданном значении x* =21.
4.5 Вычислить выборочный линейный коэффициент корреляции.
4.6 При уровне значимости α=0,05 проверить значимость коэффициента корреляции.
Решение:
1.1 Проведем группировку исходных данных, т.е. разобьем варианты на отдельные интервалы. Найдем разность между наибольшим и наименьшим значениями признака xmax-xmin = 25,92 2,41 = 23,51.
Тогда при разбивке на 8 интервалов длина интервала составит
h = 23,51/8 =2,93875 3. Получим таблицу 1.
Таблица 1
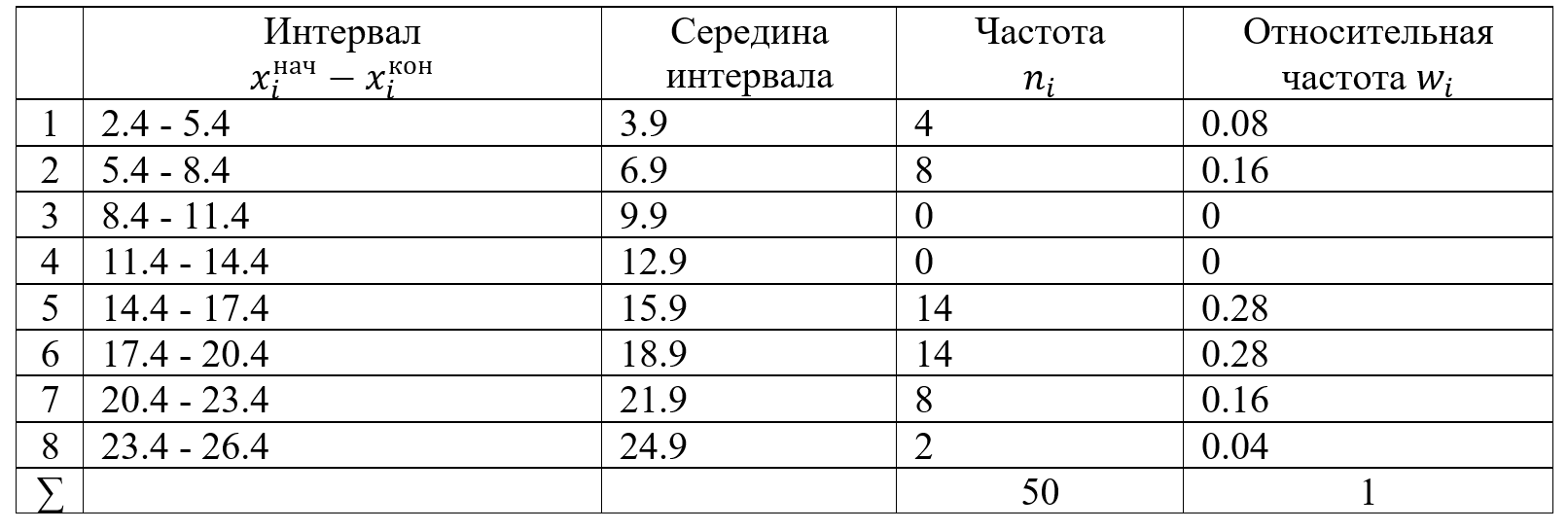
1.2 Построим для сгруппированного ряда гистограмму частот.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства