Условие задачи
Случайные величины X1 и X2 имеют биномиальное и пуассоновское распределения соответственно. Найти вероятности P(1 ≤ Xi ≤ 3), если математическое ожидание M(Xi) = 2, а дисперсия D(X1) = 3/2 = 1,5.
Ответ
Так как распределения дискретные, то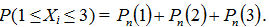 
1) Если проводится n независимых испытаний, в каждом из которых событие А происходит с вероятностью p, то вероятность того, что событие А настанет ровно k раз, равняется :
Потяни
