Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания у первого стрелка равна 0.9. у второго - 0,7, у третьего - 0,8. Найти вероятность того, что:
«Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания у первого стрелка равна 0.9. у второго - 0,7, у третьего - 0,8. Найти вероятность того, что:»
- Теория вероятностей
Условие:
Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания у первого стрелка равна 0.9. у второго - 0,7, у третьего - 0,8.
Найти вероятность того, что: а) мишень не будет поражена; б) в мишени будет хотя бы одна пробоина; в) в мишени будет только одна пробоина.
Решение:
Пусть А первый стрелок попал,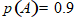 
, В второй стрелок попал, 
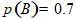, С третий стрелок попал
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э